Bogen- und Hängeträger
[444] Bogen- und Hängeträger (arches and suspension girders; poutres en arcs et poutres suspendues; travi in arco et travi sospesi), Tragwerke, die dadurch gekennzeichnet sind, daß auch bei lotrechter Belastung in ihren Auflagerpunkten schief gerichtete Kräfte auftreten, wodurch sie sich von den nur lotrechte Auflagerdrücke äußernden Balkenträgern unterscheiden. Bei den Bogenträgern ist die Auflagerkraft nach außen, bei den Hängeträgern nach dem Innern der lichten Weite gerichtet; es entsteht sonach bei den ersteren ein Horizontalschub, bei den letzteren ein Horizontalzug. Das Auftreten dieser wagrechten Kräfte ist durch die Unverschiebbarkeit der Auflagerpunkte (bei den Bogenträgern Kämpfer genannt) bedingt. Diese werden entweder direkt auf die angrenzenden Stützen übertragen oder durch anschließende ähnliche Träger mit gemeinschaftlichem Auflager bis an die festen Enden der Konstruktion fortgepflanzt und hier durch die Standfestigkeit der stützenden Körper (Widerlager bei den Bogenträgern, Verankerungen bei den Hängeträgern) aufgenommen. Man kann den Horizontalschub der Bogenträger aber auch durch ein die Bogenfüße verbindendes Zugband aufnehmen lassen, in welchem Falle dann die Stützen nur lotrechte Belastungen erfahren.
Die Bogenträger und die Hängeträger können rücksichtlich ihrer geometrischen Form als Spiegelbilder aufgefaßt werden; sie unterscheiden sich nach obigem nur durch das Vorzeichen der horizontalen Auflagerkraft und ihre Berechnung kann daher auch nach den gleichen Grundsätzen erfolgen.[444]
Die hierhergehörigen Trägersysteme lassen sich zunächst in zwei Gruppen sondern, in die schlaffen Spreng- und Hängewerke und in die steifen oder versteiften Bogen- und Hängeträger. Schlaff nennt man eine Trägerkonstruktion, wenn ihre geometrische Gestalt nicht festgelegt ist, sondern mit der Lastverteilung wechselt. Diese Eigenschaft besitzt die Kette, das Seil und auch das Vielecksprengwerk aus gelenkartig verbundenen Stäben; während aber das schlaffe Hängewerk seine Form wirklich der Belastung anpassen kann, vermag das Sprengwerk nur eine labile Gleichgewichtslage anzunehmen, d.h. es stürzt bei einer Änderung der Belastung in sich zusammen. Das schlaffe Sprengwerk ist daher als Trägerkonstruktion nicht brauchbar und auch das schlaffe Hängewerk ist für Brücken, die unter wechselnder Verkehrslast nur geringe Formveränderungen erleiden sollen, von vornherein ausgeschlossen.
Die Versteifung der schlaffen Systeme kann erreicht werden, entweder durch ihre Verbindung mit einem Balkenträger (schlaffe Bogen oder Ketten mit Versteifungsträger) oder dadurch, daß man sie selbst steif ausbildet. (Elastische Bogen, Bogen- und Hängefachwerke.)
Theorie der B.
A. Der elastische Bogen über einer Öffnung. Man versteht darunter einen eben gekrümmten Stab, der mit seinen Enden unverschieblich gelagert ist. Sind die festgehaltenen Enden (Kämpfer) frei drehbar, so hat man es mit einem gelenkig gelagerten Bogen oder einem Bogen mit Kämpfergelenken zu tun; sind dagegen die Stabenden auch an ihrer Drehung vollständig behindert, so entsteht der eingespannte oder gelenklose Bogen. Den auf einen solchen Bogenträger angreifenden äußeren Kräften halten die Gegenkräfte der Stützen (Kämpferdrücke) das Gleichgewicht. Zu ihrer Festlegung sind im allgemeinen 6 Bestimmungsstücke (Größe, Richtung und Lage einer jeden Kämpferkraft) erforderlich, von denen drei durch die Gleichgewichtsbedingungen des ebenen Kräftesystems bestimmt sind. Für den eingespannten Bogen fehlen sonach zur Ermittlung der Kämpferkräfte drei, auf statischem Wege nicht mehr erhältliche Bestimmungsstücke; das Trägersystem ist dreifach statisch unbestimmt. Beim gelenkig gelagerten Bogen vermindert sich die Zahl der Unbestimmtheiten auf eine, da durch die Festlegung der Stützpunkte zwei Bedingungen für die Lage der Kämpferdrücke geschaffen werden. Durch Anbringung eines Mittelgelenkes endlich, d.i. durch den Dreigelenkbogen, erzielt man volle statische Bestimmtheit, die Zerlegung der Resultierenden der am Bogen angreifenden Kräfte in die beiden Kämpferdrücke ist hier nur in eindeutiger Weise möglich. In den Fällen der statischen Unbestimmtheit dagegen sind die auftretenden Kräfte durch die elastischen Formänderungen bedingt und aus ihnen abzuleiten.
Innere Kräfte des massiven Bogens. Führt man durch den Bogen einen beliebigen Querschnitt senkrecht zu seiner Schwerachse und setzt die auf den abgetrennten rechten oder linken Bogenteil einwirkenden äußeren Kräfte, einschließlich der Kämpferkraft, zu einer Resultierenden zusammen, so gibt diese die Beanspruchung des betreffenden Querschnittes, in dem sie Normal- und Schubspannungen hervorruft. Letztere werden bei einer der Belastung richtig angepaßten Bogenform nur klein und kommen bei der Berechnung eines massiven oder Vollwandbogens nicht wesentlich in Betracht. Die Normalspannungen hängen von der zum Querschnitt senkrechten Komponente N der äußeren Kraft ab, und man legt ihrer Verteilung über den Querschnitt die für elastische Baustoffe geltenden Gesetze zu gründe. Man kann diese Annahme sowohl für eiserne Bogen (Blechbogen) wie auch mit praktischer Zulässigkeit für Stein- und Mauerwerkbogen gelten lassen, sonach die Bogenträgertheorie auch auf die Gewölbe anwenden (s. Gewölbe).
Unter der Voraussetzung, daß der Krümmungshalbmesser eines stabförmigen Bogens im Verhältnis zur Höhe seines Querschnittes groß ist, gelten für den gekrümten Stab mit großer Annäherung dieselben Formeln wie für den geraden Stab, der auf zusammengesetzte Normal- und Biegungsfestigkeit beansprucht wird. Bezeichnet nämlich N die im Stab wirkende Achsialkraft, M das auf den Schwerpunkt des Querschnittes, dessen Fläche F und dessen Trägheitsmoment J sei, bezogene Biegungsmoment der äußeren Kräfte, so berechnet sich die Normalspannung für eine im Abstand v von der Schwerpunktsachse gelegene Faser aus
1)
Hierin kann N und M allgemein mit dem gleichen Vorzeichen eingeführt werden und ist v für jene Punkte des Querschnittes positiv, die mit N auf derselben Seite der Schwerpunktachse liegen.
Die Randspannungen, d. s. die Spannungen in der obersten und untersten Faser, deren[445] Abstände von der Schwerachse a1 und a2 sein mögen, ergeben sich hieraus mit
2)
oder durch die auf die Kernpunkte bezogenen Momente Mu und Mo ausgedrückt, mit
2a
Die Kernpunkte sind bestimmt durch die Kernpunktabstände (Abb. 230) ku = J/Fa1 und ko = J/Fa2. Für einen Rechteckquerschnitt von der Höhe h ist ku = ko = 1/6 h, die Kernpunkte entsprechen den Drittelpunkten der Höhe. Für den  -Querschnitt sind die Kernpunktabstände größer. Die Größtwerte der Randspannungen bestimmen sich sonach gemäß Gleichung 2 a aus den Größtwerten der auf die Kernpunkte bezogenen Biegungsmomente. Ist der Querschnitt gegeben, so unterliegt die Ermittlung der Randspannungen auf Grund der Gleichung 2 oder 2a keiner Schwierigkeit; handelt es sich aber um die Dimensionierung eines Blechbogens, so können diese Formeln nicht unmittelbar verwendet werden, da bei unsymmetrischer Ausbildung des Querschnittes (verschiedener Stärke der beiden Gurtungen) die Lage des Schwerpunktes (zur Anwendung der Gleichung 2) oder die Lage der Kernpunkte (zur Anwendung der Gleichung 2a) nicht bekannt ist.
-Querschnitt sind die Kernpunktabstände größer. Die Größtwerte der Randspannungen bestimmen sich sonach gemäß Gleichung 2 a aus den Größtwerten der auf die Kernpunkte bezogenen Biegungsmomente. Ist der Querschnitt gegeben, so unterliegt die Ermittlung der Randspannungen auf Grund der Gleichung 2 oder 2a keiner Schwierigkeit; handelt es sich aber um die Dimensionierung eines Blechbogens, so können diese Formeln nicht unmittelbar verwendet werden, da bei unsymmetrischer Ausbildung des Querschnittes (verschiedener Stärke der beiden Gurtungen) die Lage des Schwerpunktes (zur Anwendung der Gleichung 2) oder die Lage der Kernpunkte (zur Anwendung der Gleichung 2a) nicht bekannt ist.
Man kann hier das folgende Näherungsverfahren einschlagen: Es wird ein Grundquerschnitt (Abb. 231), aus Stehblech und Winkeleisen bestehend, angenommen; man wählt seine Höhe bei Blechbogen für Brückenträger mit 1/40–1/60 der Stützweite. Dessen Fläche sei = Fo, Trägheitsmoment für die horizontale Schwerachse = Jo, Höhe = h. Man bestimmt nun die größten Biegungsmomente Mu und Mo in bezug auf die Flanschenflächen der Winkeleisen und erhält dann, wenn s die größte zulässige Druckspannung im Querschnitt bezeichnet, seine erforderliche Fläche aus
3)
Die Querschnittsflächen der beiden Gurtungslamellen folgen hiermit aus
4)
Für die Berechnung der Größtwerte von Mo und Mu wird es zumeist genügen, die ungünstigste Belastungsweise für den in der Stabachse gelegenen Querschnittpunkt zu grunde zu legen, wodurch die Zahl der in Betracht kommenden Belastungsfälle auf die Hälfte vermindert wird.
Mit Hilfe der nach dieser ersten Näherung entwickelten Querschnitte kann nunmehr (was aber selten notwendig werden wird), eine genauere Berechnung erfolgen, indem man die Kernlinien ermittelt, die Maximalmomente nun auf diese bezieht und dann zur Berechnung von fo und fu wieder die obigen Formeln anwendet.
Die äußeren Kräfte der Bogenträger. Für den allgemeinen Fall des eingespannten, gelenklosen Bogens, der durch beliebige lotrechte Kräfte belastet ist (Abb. 232), seien H der auftretende Horizontalschub, V1 und V2 die Vertikalkomponenten der Stützenreaktionen, M1 und M2 die Biegungsmomente in den Einspannungsstellen.
Denkt man sich H, M1 und M2 gleich Null, so geht der Bogenträger in einen frei aufliegenden Balken über und man kann für diesen das Biegungsmoment  x in einem Querschnitt im Anstand x vom linken Kämpfer, sowie den linksseitigen Stützendruck
x in einem Querschnitt im Anstand x vom linken Kämpfer, sowie den linksseitigen Stützendruck 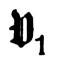 berechnen. Hiermit erfolgt aber dann das Biegungsmoment für den Bogenträger aus
berechnen. Hiermit erfolgt aber dann das Biegungsmoment für den Bogenträger aus
5)
der Vertikaldruck im Kämpfer aus
6)
Konstruiert man mit einer Poldistanz H das Seilpolygon der Belastungskräfte und bringt[446] dieses in eine solche Lage zu dem Bogen, daß die Schnittpunkte mit den Kämpfervertikalen um e1 = M1/H und e2 = M2/H über den Kämpferpunkten liegen, so entsprechen die mit H multiplizierten Vertikalabstände des Seilpolygons von der Bogenachse, bzw. von den Kernlinien den auf den Bogenträger einwirkenden Biegungsmomenten (Abb. 232).
Es ist sonach bei dem eingespannten Bogen zur vollständigen Bestimmung der äußeren Kräfte und damit auch der inneren Spannungen die Kenntnis dreier Auflagergrößen erforderlich; bei dem Bogen mit Kämpfergelenken werden die Einspannungsmomente Null und erübrigt in diesem Fall bloß die Bestimmung des Horizontalschubs.
Besteht die Belastung des Bogens aus einer einzelnen Last, so schneiden sich die Richtungen der Kämpferdrücke auf der Angriffslinie der Last und es beschreibt dieser Schnittpunkt C bei einer Veränderung der Lage der Last eine Kurve, die sog. Kämpferdrucklinie (Abb. 233). Die Richtungen der Kämpferdrücke umhüllen dabei bestimmte Linien, die Kämpferdruckumhüllungslinien genannt werden. Für den Bogen mit Kämpfergelenk schrumpfen diese letzteren in die Kämpferpunkte zusammen, da hier die Richtungen der Kämpferdrücke stets durch die Kämpfergelenke hindurchgehen müssen.
Hat der Bogen auch noch ein Scheitelgelenk, so muß die Richtung eines Kämpferdruckes überdies auch noch durch das Scheitelgelenk hindurchgehen und es besteht in diesem Fall die Kämpferdrucklinie aus zwei Geraden, die sich als die Verlängerungen der Verbindungssehnen des Scheitelgelenkes mit den beiden Kämpfergelenken darstellen.
Ungünstigste Belastungen. Mit Hilfe der Kämpferdruck- und Kämpferdruckumhüllungslinien läßt sich der Einfluß der Lastlage auf das Vorzeichen der Spannungen in einem bestimmten Querschnitt untersuchen. Für die Normalspannungen im unteren Querschnittsrande ziehe man durch den oberen Kernpunkt des betreffenden Querschnittes Tangenten an die Kämpferdruckumhüllungen, so bestimmen diese in den Schnittpunkten J1 oder J2 (Abb. 234) mit der Kämpferdrucklinie die Belastungsscheiden, da eine jede in J1 und J2 angreifende Last in Beziehung auf den Kernpunkt K2 kein Moment, mithin in der unteren Querschnittsfaser keine Spannung zur Folge hat. Beim Übergang der Last über die Punkte J1 und J2 ändert sonach die Spannung σu ihr Vorzeichen. Für die obere Faser tritt der untere Kernpunkt K1 an die Stelle und man erhält für diesen die Belastungsscheiden J3 und J4. (In der Abbildung fällt der Punkt J4 bereits außerhalb der Spannweite, es ist sonach nur eine Belastungsscheide vorhanden.) Mit entsprechender Berücksichtigung des Vorzeichens des Moments lassen sich sonach die folgenden Regeln aufstellen:
Die Spannung σo wird ein Zug für jede Last in der Strecke i3 b, ein Druck für jede Last in der Strecke a i3; die Spannung σu wird ein Zug für jede Last in der Strecke i1 i2, ein Druck für jede Last in der Strecke a i1 und i2 b.
Ähnliche Regeln lassen sich auch für die Scherkräfte aufstellen. Die Scherkraft in einem Querschnitt wird erhalten, wenn man die auf diesen einwirkende äußere Kraft (Resultierende aus den Auflagerkräften und den Belastungen zwischen Kämpfer und Querschnitt) in eine auf der Ebene des Querschnittes senkrechte Komponente (Längs- oder Achsialkraft) und in eine in den Querschnitt fallende Komponente zerlegt. Letztere gibt die Scher- oder Querkraft; man zählt diese, wie bei den Balkenträgern, positiv, wenn sie auf den linken Trägerteil nach aufwärts wirkt. – Zieht man (Abb. 235) die Lotrechte CF1 durch den oberen Querschnittsrand C und parallel zur Tangente in M an die Stabachse eine Tangente[447] an die Kämpferdruckumhüllungslinie, so geben wieder die Schnittpunkte F1 und F2 mit der Kämpferdrucklinie die Belastungsscheiden.
Die Querkraft in M wird positiv für jede Last in der Strecke f1 f2, negativ für jede Last in der Strecke a f1 und f2 b.
Bei einem Bogen mit Kämpfergelenken sind anstatt der Tangenten an die Kämpferdruckumhüllungskurven die Linien durch die Kämpfergelenke zu legen.
a) Bogenträger mit drei Gelenken.
Bei Vorhandensein von Kämpfergelenken lautet Gleichung 5)
7)
Die Anbringung eines dritten Gelenkes in einem Punkt mit der Ordinate y = f liefert zufolge der Bedingung, daß für den Gelenkpunkt das Moment Null werden muß, die Gleichung 0 =  g – H f, voraus
g – H f, voraus
8)
Hierin bezeichnet  g das auf das Mittelgelenk bezogene Moment des gleich belasteten Balkenträgers. Die Einflußlinie von H, d.i. eine Linie, deren Ordinaten die Größe von H für eine wandernde Einzellast G angeben, stimmt sonach mit der Einflußlinie des Momentes
g das auf das Mittelgelenk bezogene Moment des gleich belasteten Balkenträgers. Die Einflußlinie von H, d.i. eine Linie, deren Ordinaten die Größe von H für eine wandernde Einzellast G angeben, stimmt sonach mit der Einflußlinie des Momentes  g überein. Sie wird durch die in Abb. 236 angedeutete Konstruktion in der Dreiecklinie a c b erhalten.
g überein. Sie wird durch die in Abb. 236 angedeutete Konstruktion in der Dreiecklinie a c b erhalten.
Die Biegungsmomente, die auf die Kernpunkte der Querschnitte zu beziehen sind, berechnen sich aus Gleichung 7. Man kann diese auch schreiben
und hiernach wieder die Einflußlinie, die die Veränderlichkeit des Momentes für eine wandernde Einzellast angibt, konstruieren (Abb. 237). Die Größe  läßt sich nämlich durch die Ordinaten der Linie a m b darstellen, die man durch die in Abb. 237 angegebene Konstruktion erhält. Der unter einer Einzellast G gemessene lotrechte Abstand der beiden Polygone a c b und a m b gibt dann mit der Ordinate y des Bogenpunktes M multipliziert das in diesem Punkt auftretende Biegungsmoment.
läßt sich nämlich durch die Ordinaten der Linie a m b darstellen, die man durch die in Abb. 237 angegebene Konstruktion erhält. Der unter einer Einzellast G gemessene lotrechte Abstand der beiden Polygone a c b und a m b gibt dann mit der Ordinate y des Bogenpunktes M multipliziert das in diesem Punkt auftretende Biegungsmoment.
Der Schnittpunkt i liegt in der Lotrechten durch J und bestimmt die Belastungsscheide. Die größten positiven Momente treten bei Belastung der Strecke a i, die größten negativen Momente bei jener von i b auf.
Für eine gleichmäßig verteilte Last p für die Längeneinheit berechnen sich mit Einführung der Abszisse λ, des Punktes J
die größten und kleinsten Werte der Momente für den Punkt x y aus
9)
Ist die Bogenachse parabolisch, so wird für jeden Punkt der Bogenachse Mmax = – Mmin und es wird in diesem Falle bei Belastung der halben Spannweite (mit λ1 = l/2) in der belasteten, bezw. unbelasteten Bogenhälfte
für den Punkt im Viertel der Spannweite sonach M = ± 1/64 pl2 Das absolut größte Moment tritt aber im Abstande x = 0∙234 l auf und wird abs. max M = ± 0∙01883 pl2.
Die Scherkräfte im Querschnitt M folgen aus Q = Vcosφ – H sinφ und es läßt sich[448] die Einflußlinie für eine wandernde Einzellast, wie Abb. 238 zeigt, darstellen. Es geben die lotrechten Abstände des Polygons a t s b und der Horizontalschublinie a c b mit sin φ multipliziert die Scherkraft. Bei gleichmäßig verteilter Belastung berechnen sich wieder die Größtwerte aus
10)
wenn
gesetzt wird. Für jene Querschnitte, für die sich λ2 > l/2 ergeben würde, ist in den obigen Formeln
λ2 = l
zu setzen.
Hinsichtlich der Durchbiegungen seien hier bloß jene Formeln mitgeteilt, die sich auf die Scheitelsenkung eines Bogens mit parabolischer Achse und konstantem Querschnitt beziehen. Es bezeichnen F den Bogenquerschnitt, J dessen Trägheitsmoment, E den Elastizitätskoeffizienten, dann bewirkt eine im Abstande ξ < l/2 vom Kämpfer angreifende Last G im Scheitel des Bogens eine Senkung
11)
Die größte Senkung bei gleichmäßig verteilter Belastung findet statt, wenn annähernd das mittlere Drittel der Spannweite belastet ist, u. zw. wird
12)
Die größte Hebung des Bogenscheitels tritt ein, wenn annähernd das erste und letzte Drittel der Spannweite belastet ist, und wird
13)
Durch eine Temperaturzu- oder -abnahme um t0 hebt oder senkt sich der Bogenscheitel um
14)
wenn ω = 0∙0000124 den Ausdehnungskoeffizienten des Eisens und b die Bogenlänge bezeichnet.
Die größte horizontale Verschiebung des Scheitels bei Belastung der halben Spannweite wird
15)
b) Bogen mit Kämpfergelenken. Hier ist die Bestimmungsgleichung für den Horizontalschub aus den elastischen Formänderungen des Bogens abzuleiten. Mit der zulässigen Annäherung, die Längskraft im Bogen konstant und gleich dem Horizontalschub H zu setzen und mit Einführung eines mittleren Querschnittes F0 erhält man den allgemeinen Ausdruck
16)
Hierin bezeichnet wieder  das Biegungsmoment für den frei aufliegenden Balkenträger, b die Bogenlänge, β den Winkel der Tangente im Kämpfer mit der Horizontalen, und es bestimmt das erste Glied im Zähler des obigen Ausdruckes die Wirkung einer Belastung, das zweite Glied jene einer Temperaturerhöhung gegen den spannungslosen Zustand um t0 und das dritte Glied die Wirkung einer Verschiebung der Kämpferpunkte, durch welche sich die Spannweite um ∆ l vergrößern würde.
das Biegungsmoment für den frei aufliegenden Balkenträger, b die Bogenlänge, β den Winkel der Tangente im Kämpfer mit der Horizontalen, und es bestimmt das erste Glied im Zähler des obigen Ausdruckes die Wirkung einer Belastung, das zweite Glied jene einer Temperaturerhöhung gegen den spannungslosen Zustand um t0 und das dritte Glied die Wirkung einer Verschiebung der Kämpferpunkte, durch welche sich die Spannweite um ∆ l vergrößern würde.
Besteht die Belastung bloß aus einer Einzellast G im Punkte M des Bogens (Abb. 239), so kann der von ihr erzeugte Horizontalschub auch durch graphische Konstruktion gefunden werden. Es stellt nämlich
das Gfache Moment eines Balkenträgers von der Stützweite l im Punkte M dar, den man sich mit
stetig verteilt belastet denkt. Man erhält dieses durch Verzeichnung des entsprechenden Seileckes. Desgleichen ist
das Moment der an den Bogenpunkten angreifenden, parallel zur Kämpfersehne gerichteten[449] Kräfte y/Jcosφ und wird demnach ebenfalls durch ein Seileck erhalten. Beide Seilecke sind aus der gleichen, beliebigen Polweite p zu konstruieren und es ist der Abschnitt des zweiten Seileckes auf der Kämpfersehne noch um die kleine Größe
zu verbessern. Nimmt man die Strecke n0 n1, als Lastgröße G an, so bestimmt die Ordinate des ersten Seileckes im Punkte M die Größe des Horizontalschubes. Es ist sonach dieses Seileck, bzw. die von ihm eingehüllte Seilkurve die Einflußlinie des Horizontalschubes. Überträgt sich die Belastung nur in einzelnen Punkten durch Vertikalständer auf den Bogen, so tritt an Stelle der Kurve das eingeschriebene Vieleck, dessen Ecken auf den Lotrechten durch die direkt belasteten Punkte liegen.
Für einen Bogen mit flacher parabolischer Achse und nahezu konstantem Trägheitsmoment (Blechbogen mit parallelen Gurtungen) folgt der Horizontalschub für eine im Abstand ξ vom Kämpfer angreifende Einzellast G aus
17)
worin
oder mit Vernachlässigung der Wirkung der Achsialkraft angenähert f` = f zu setzen ist. Man kann für diese Horizontalschublinie mit großer Annäherung eine Parabel mit der Pfeilhöhe
G setzen, demnach den Horizontalschuh durch
17a)
ausdrücken. Der Fehler gegenüber der genaueren Formel beträgt für eine Last im Scheitel rund 4%.
Mit Hilfe der Einflußlinie des Horizontalschubes lassen sich nun die Einflußlinien der Biegungsmomente (Abb. 240) und der Querkräfte in ganz derselben Weise darstellen wie für den Bogen mit drei Gelenken (Abb. 237). Es tritt nur an Stelle der Horizontalschublinie für den Bogen mit drei Gelenken jene für den Bogen mit zwei Gelenken. Zur Berechnung der größten Momente im Punkt x, y bei gleichmäßig verteilter Last p für die Längeneinheit können die nachstehenden Formeln dienen.
18)
worin für flache Bogen mit konstantem Querschnitt λ aus
19)
und
20)
einzusetzen ist. Für die mittlere Strecke beiderseits des Bogenscheitels zwischen den Abszissen x` und l – x`, die durch die Gleichung
bestimmt sind, ist zu dem oben berechneten Werte von M noch jener zu addieren, der sich aus derselben Formel für den symmetrisch gelegenen Bogenpunkt ergibt. Das Moment bei totaler Belastung wird
21)
woraus das größte positive Moment
Mmax = M – Mmin
folgt.
Bei dem statisch nicht bestimmten Bogen werden auch durch Temperaturänderungen Spannungen hervorgerufen. Für eiserne Tragwerke hat man diese Temperaturänderungen mit mindestens t = ± 30° anzusetzen und erhält dann mit
E ω = 2,000.000 × 0∙0000124 = 248
(auf m und t als Einheit bezogen), also mit E w t = 7440 den Horizontalschub eines flachen Bogens infolge Temperaturveränderung
22)
Die hierdurch hervorgerufenen Momente bestimmen sich aus
Mt = – Ht y 23)
Die infolge dieser Temperaturwirkung auftretenden Spannungen können unter Umständen ziemlich beträchtlich werden. Für einen aus zwei Gurtungen von gleichem Querschnitt und dem Abstand h bestehenden Bogen wird die Temperaturspannung im Bogenscheitel des Ober- und Untergurtes
[450] für ein Verhältnis h/f = 1/3 würde
σ0 = ± 185 kg und σu = ± 259 kg.
Die Durchbiegung im Scheitel eines flachen Parabelbogens von konstantem Querschnitte wird für eine im Abstand ξ vom Kämpfer liegende Last G
24)
Die größte Senkung findet wieder statt, wenn ungefähr das mittlere Drittel der Spannung belastet ist; hierfür wird
25)
Die Scheitelbewegung infolge Temperaturänderung um t0 beträgt
26)
c) Bogen ohne Gelenk. Der Horizontalschub infolge Belastung ist wieder durch eine ganz analoge Formel wie beim Zweigelenkbogen (16) bestimmt, nämlich
27)
nur bezieht sich jetzt die Ordinate y der Bogenachspunkte nicht auf die Kämpfersehne, sondern auf eine zu ihr parallele Achse, die so gelegen ist, daß
Hat der Bogen ein annähernd konstantes Trägheitsmoment, so daß J cos φ = J` = konstant ist, so wird obiger Bedingung durch eine Gerade entsprochen, die die Fläche zwischen Bogenachse und Bogensehne in ein flächengleiches Rechteck verwandelt. Bezeichnet t0 den Abstand dieser Achse von der Bogensehne, so werden bei einem Bogen mit konstantem Trägheitsmomente die Einspannungs-(Kämpfer-) Momente für eine im Abstand ξ vom linken Kämpfer gelegene Last G
28)
Für den flachen Parabelbogen wird mit
insbesondere
29)
30)
Hiermit bestimmen sich die Biegungsmomente für den Bogen nach Gleichung 5).
Ist der Bogen in der Strecke λ vom linken Kämpfer aus mit p f. d. Längeneinheit belastet, so ergibt sich für den flachen Parabelbogen:
31)
32)
Das größte positive Moment in einem Punkte mit den auf dem Kämpfer A bezogenen Koordinaten xkyk wird
33)
Die Laststrecke λ ist hierbei aus
34)
zu bestimmen. Für totale Belastung wird
35)
womit Mmin = M – Mmax. Der Größtwert des Moments auf den ungefähr im Viertel der Spannweite gelegenen Punkt der parabolischen Bogenachse wird rund 1/100 pl2.
Der infolge Temperaturänderung um
t = ± 30°
entstehende Horizontalschub wird
36)
sonach ungefähr sechsmal größer als beim Bogen mit Kämpfergelenken. Besteht der Bogen aus gleichen Gurtungen im Abstand h, so wird die Temperaturspannung im Scheitel des Bogens
und im Kämpfer
[451] Die Temperaturspannungen werden sonach im allgemeinen beträchtlich größer als bei dem Bogen mit Kämpfergelenken.
B. Gitter- oder Fachwerksbogen.
Die hierhergehörigen Fachwerksträger sind durch das Auftreten von horizontalen Auflagerkräften als Bogen, bzw. Hängewerke gekennzeichnet; sie bestehen immer aus zwei Gurtungen, von denen mindestens eine gekrümmt, bzw. polygonal ist und die durch eine Ausfachung (Gitterwerk) miteinander verbunden sind. Die Berechnung der Stabkräfte hat nach der allgemeinen Fachwerkstheorie zu geschehen, die von der vereinfachenden Annahme ausgeht, daß die Verbindung der Stäbe durch reibungslose Gelenke bewerkstelligt ist.
Sind die äußeren Kräfte, d. s. die Belastungen und die Auflagerkräfte, bekannt, so kann für einen durch das Fachwerk geführten Schnitt die Resultierende der auf den abgetrennten Trägerteil einwirkenden äußeren Kräfte bestimmt werden (Abb. 242). Diese sei R, ihre Momente auf die Knotenpunkte o und u bezogen, seien M0 und Mu. Dann sind mit den Bezeichnungen der Abbildung die Gurtspannungen
Um die größten Werte dieser Gurtspannungen zu erhalten, hat man wieder die ungünstigste Belastung anzunehmen, die sich in ganz gleicher Weise wie hinsichtlich der Momente für den vollwandigen Bogenträger bestimmt (Abb. 234). Es treten nur an Stelle der Kernpunkte K1 und K2 die beiden Momentenpunkte u und o.
Die Spannungen der Gitterstäbe werden bei parallelen, bzw. konzentrischen Gurtungen aus den Querkräften erhalten. Bei nicht parallelen Gurtungen ist der Schnittpunkt der beiden dem betreffenden Fach angehörenden Gurtstäbe als Momentenpunkt anzusehen und folgt dann die Gitterstabspannung aus
S = Mz/d.
Die Größtwerte der Spannungen werden am besten mit Hilfe von Einflußlinien erhalten. Letztere sind identisch mit den Einflußlinien für die Momente Mo, Mu und Mz und bei einem gelenkig gelagerten Bogen aus der Einflußlinie des Horizontalschubes H leicht abzuleiten, analog wie bei Vollwandbogen (Abb. 240). In Abb. 243 ist in dieser Weise die Einflußlinie der Stabkraft S des Ausfachungsstabes o, u dargestellt. Setzt man nämlich Mz =  z – Hyz, so ist
z – Hyz, so ist
Die nach dem Kraftmaßstab der H-Linie gemessenen Ordinaten der in Abb. 243 schraffierten Fläche sind sonach noch mit yz/d zu multiplizieren.
Es erübrigt nun noch zu zeigen, wie die Auflagerkräfte zu berechnen sind, deren Kenntnis im vorhergehenden vorausgesetzt wurde. Bei einem Bogen mit gelenkiger Auflagerung handelt es sich nur um Bestimmung des Horizontalschubes, um Verzeichnung der H-Linie. Diese wird beim statisch bestimmten Dreigelenkbogen wie oben angegeben (Abb. 236) erhalten. Beim Zweigelenkbogen ist der Horizontalschub aus der elastischen Formänderung abzuleiten. Hat der Bogen bei geringer Tragwandhöhe parallele Gurtungen (Abb. 244), sonach ein wenig veränderliches Trägheitsmoment, so kann mit ausreichender Annäherung dasselbe Berechnungsverfahren wie für vollwandige Bogen (Formel 16–36) in Anwendung gebracht werden. Sonst wird der überhaupt bei statisch unbestimmten Fachwerksanordnungen anzuwendende Berechnungsvorgang einzuschlagen sein. Dieser möge hier für den Bogen mit Kämpfergelenken kurz[452] angedeutet werden. Denkt man sich in der Verbindungslinie der beiden Kämpferpunkte zwei nach innen gerichtete Kräfte von der Größe = 1 wirksam (Abb. 245), so werden diese in den sämtlichen Stabgliedern Spannungen u hervorrufen, die sich ohne Schwierigkeit ermitteln lassen. Tatsächlich wirkt an den Kämpfern die Horizontalkraft H; die von ihr erzeugten Spannungen werden daher Hu. Diese treten zu den Spannungen S hinzu, die durch die äußere Belastung in dem statisch bestimmten System entstehen, d.i. wenn H = 0, d.h. wenn der Bogen horizontal verschiebbar gelagert wäre.  sind sonach die Spannungen in dem als Balkenträger aufgefaßten Fachwerk und es werden hiermit die Spannungen im Bogenfachwerk
sind sonach die Spannungen in dem als Balkenträger aufgefaßten Fachwerk und es werden hiermit die Spannungen im Bogenfachwerk
37)
Infolge dieser Spannungen finden elastische Längenänderungen in den Stabgliedern statt, die sich bei der Querschnittsfläche F und der Länge s eines Stabes, ferner dem Elastizitätskoeffizienten E mit
berechnen, wenn zur Abkürzung r = s/F gesetzt wird. Wird angenommen, daß sich die Kämpfer etwas unter der Belastung verschieben, wodurch sich die Spannweite um Δl vergrößere, so muß nach dem Satz von der Gleichheit der virtuellen Verrückungen, die Arbeit der Kräfte 1 gleich jener der von ihnen hervorgerufenen Spannungen u sein, also
Mit der Substitution von S aus Gleichung 37) und Reduktion auf H folgt schließlich
38)
In anderer Form wird H auch durch folgende Betrachtung erhalten: Wir denken uns das Bogenfachwerk als Balkenträger in einem Auflager wagrecht verschieblich und bezeichnen die Verschiebung dieses Auflagers
infolge einer Last 1, in einem beliebigen Punkt M des Bogens wirkend, mit δma
infolge der Last Pm in diesem Punkte sonach mit Pmδma
infolge einer in der Richtung der Kämpfersehne auf das bewegliche Auflager wirkender Kraft 1 mit δaa
sonach infolge der Kraft H mit Hδaa.
Die wirkliche gegenseitige Verschiebung der Kämpfer des Bogenträgers, infolge eines Hinausschiebens der Widerlager, wurde mit – Δl bezeichnet. Diese muß sich als Ergebnis der Wirkungen sämtlicher Lasten P und der Kraft H herausstellen, sonach ist
woraus
39)
Die beiden Ausdrücke 38 und 39 für H sind natürlich identisch und es ist
Gleichung 38 dient zur rechnerischen Ermittlung von H, während Gleichung 39 zu einer graphischen Bestimmung der Einflußlinie verhilft. Wirkt nämlich blos eine einzige Last P im Punkte M und ist Δl = o, so ist
Die Verschiebungsgrößen δma und δaa sind aber graphisch erhältlich. Nach dem Satze über die Gegenseitigkeit der Verschiebungen (Maxwell) ist nämlich δma = δam, d.h. die Horizontalverschiebung des Auflagers durch eine Kraft 1 in M ist gleich der lotrechten Verschiebung von M infolge einer Horizontalkraft 1 im Auflager. Diese lotrechten Verschiebungen werden durch die Biegungslinie des Fachwerks für H = 1 erhalten und es gibt diese Biegungslinie schon die Einflußlinie für H, wenn die Lastgröße durch δaa dargestellt wird. Die Biegungslinie eines Fachwerks kann durch Zeichnung eines Verschiebungsplanes (Williotplanes) oder als Seileck aus den Winkeländerungen des Fachwerks erhalten werden (s. Durchbiegung).
Kennt man H, so sind durch Gleichung 37) auch die Spannungen S bestimmt und man kann auch deren Einflußlinien darstellen. Die Wirkung einer Temperaturänderung um t° ergibt sich aus
40)
Zur Berechnung des statisch unbestimmten Fachwerksbogens ist eine vorläufige Annahme der Querschnittsflächen der Stäbe notwendig. Man kann sich in der Regel bei der ersten Annäherung damit begnügen, bloß die Formänderungen der Gurtungsstäbe zu berücksichtigen und kann jene der Gitterstäbe vernachlässigen. Es genügt auch, für die erste Berechnung die Gurtquerschnittsflächen konstant und im Ober- und Untergurt gleich groß anzunehmen.[453]
Die angegebene Berechnungsweise gilt natürlich ebenso für die Bogenfachwerke wie für Fachwerkshängeträger. Die letzteren bilden gewöhnlich eine durchgehende Tragkonstruktion über drei Öffnungen (Abb. 246). Ist ein Mittelgelenk vorhanden, so rechnet sich der Träger der Mittelöffnung als ein gewöhnlicher umgekehrter Dreigelenkbogen, der seinen Schub auf die Seitenträger überträgt. Letztere wirken für ihre eigene Belastung als Balkenträger, für den Träger der Mittelöffnung ist ihre Belastung ohne Einfluß. Ist der Träger ohne Gelenk durchgeführt, so sind die Formänderungen der Seitenöffnungen mit zu berücksichtigen. Bezeichnen  ,
,  ',
',  '' die Stabkräfte in den als Balkenträger aufgefaßten Systemen des 1., 2., 3. Feldes infolge der äußeren Belastung, u, u', u'' die Stabkräfte infolge der Horizontalkräfte 1, bzw. infolge der Kräfte 1 sec α in Richtung der unter dem Winkel α geneigten Verbindungslinie der Stützpunkte, so ist
'' die Stabkräfte in den als Balkenträger aufgefaßten Systemen des 1., 2., 3. Feldes infolge der äußeren Belastung, u, u', u'' die Stabkräfte infolge der Horizontalkräfte 1, bzw. infolge der Kräfte 1 sec α in Richtung der unter dem Winkel α geneigten Verbindungslinie der Stützpunkte, so ist
Es entsteht sonach bei Belastung eines jeden Feldes eine Horizontalkraft, d.i. ein Zug in der Verankerung. Die Stabkräfte ergeben sich damit aus S =  + Hu, S' =
+ Hu, S' =  ' + Hu' ...
' + Hu' ...
C. Der schlaffe Bogen oder die Kette mit Versteifungsträger.
Um die mit der Belastung wechselnde Form einer Kette oder eines Seiles zu fixieren und die Formänderungen in den Grenzen der elastischen Deformationen zu halten, verbindet man die Kette mittels Hängestangen mit einem geraden Balken (Versteifungsträger). Dieses System der Versteifung hat in einigen Fällen auch für schlaffe Bogen Anwendung gefunden, doch finden wir es hauptsächlich bei den Hängebrücken (s.d.) vertreten. In der Berechnung ist kein wesentlicher Unterschied gegenüber dem an sich steifen Bogen, vorausgesetzt, daß der Täger hinreichend steif, d.h. mit entsprechend großem Querschnittsträgheitsmoment ausgeführt ist, so daß Formänderungen bei der statischen Spannungsberechnung unberücksichtigt bleiben können. Ist H der Horizontalzug in der Kette, y die Kettenordinate von der Verbindungslinie der Aufhängepunkte gerechnet (Abb. 247), so wird das auf einem Querschnitt des Versteifungsträgers im Abstand x vom Auflager entfallende Biegungsmoment wieder
41
wenn  das Moment für den freien Balkenträger, das also beim Nichtvorhandensein der Kette auftreten würde, bezeichnet. Desgleichen wird die Querkraft im Balken
das Moment für den freien Balkenträger, das also beim Nichtvorhandensein der Kette auftreten würde, bezeichnet. Desgleichen wird die Querkraft im Balken
42
Ist im Versteifungsträger ein Gelenk angebracht und beziehen sich hierauf die Größen  0 und f, so bestimmt sich die Horizontalkraft in der Kette aus
0 und f, so bestimmt sich die Horizontalkraft in der Kette aus
43
Ist dagegen der Versteifungsträger durch kein Gelenk unterbrochen, so ist die Horizontalkraft H in analoger Weise, wie beim steifen Zweigelenkbogen, aus den elastischen Formveränderungen zu berechnen. Nimmt man eine parabolische Kettenform und ein konstantes Trägheitsmoment des Versteifungsträgers an und vernachlässigt man den Einfluß der Längendehnung der Hängestangen, so ergibt sich für eine im Abstand ξ vom Auflager angreifende Last G der Horizontalzug nach Gleichung 17)
worin
Es bezeichnet darin J das Trägheitsmoment des Versteifungsträgers, l dessen Stützweite, F die Querschnittsfläche der Kette und L ihre totale Länge zwischen den Verankerungspunkten.
Hat man die Einflußlinie der Horizontalkraft bestimmt, so lassen sich die größten Spannungen im Versteifungsträger unschwer und in ganz ähnlicher Weise wie oben für den steifen Bogen gezeigt wurde, ermitteln.
Der Versteifungsträger mit Mittelgelenk und parabolischer Kette hat in jedem Querschnitte ein ebenso großes positives wie negatives Moment aufzunehmen. Der Größtwert (bei x = 0∙234 l) ist ± 0∙01883 p l2 Bei totaler gleichmäßiger Belastung ist er nicht beansprucht. Beim Versteifungsträger ohne Gelenk werden die negativen Momente etwas kleiner, die positiven[454] Momente infolge der Längendehnung der Kette jedoch größer. Bei diesem rufen auch Temperaturänderungen Spannungen hervor, die sich in analoger Weise wie beim Bogen mit Kämpfergelenken berechnen.
Hat der Versteifungsträger nur ein verhältnismäßig kleines Trägheitsmoment, sonach große Biegsamkeit, so gibt obige Berechnungsweise nur Näherungswerte und es muß dann eine genauere Theorie mit Berücksichtigung der Formänderungen in Anwendung kommen (Manhattan-Brücke).
Literatur: Ritter, Der elastische Bogen. Zürich 1886. – Weyrauch, Elastische Bogenträger. München 1897. – Müller-Breslau, Graphische Statik der Baukonstruktionen. II, Leipzig 1903; Die neueren Methoden der Festigkeitslehre. Leipzig 1904. – Melan, Theorie der Bogen- und Hängebrücken, in Handbuch der Ing.-Wissenschaften. 2. Bd. 5. Abt. 3. Auflage. Leipzig 1906.
Melan.
Brockhaus-1809: Das Bogen-Clavier
Brockhaus-1911: Bausch und Bogen · Davyscher Bogen · Voltascher Bogen · Bogen · Bogen [2]
Herder-1854: Bausch und Bogen · Bogen
Lueger-1904: Bogen- und Zeitmaß · Durchlaufende Träger, Balken, Bogen · Bogen, kontinuierliche · Gotischer Bogen · Einhüftiger Bogen · Einfacher Bogen · Bogen [2] · Bogen [1] · Bogen mit Zugstange · Bogen, einfache · Bogen, durchlaufende · Bogen [3]
Meyers-1905: Bogen, elektrischer · Hoher Bogen · Voltascher Bogen · Bogen [4] · Bogen [1] · Bogen [2] · Bogen [3]
Pierer-1857: Gothischer Bogen · Gebürstete Bogen · Flacher Bogen · Hohe Bogen · Vorgesprengter Bogen · Scheitrechter Bogen · Maurische Bogen · Bogen-Indianer · Bogen [2] · Bogen [1] · Bausch u. Bogen · Bogen [3] · Bogen [6] · Bogen [5] · Bogen [4]
Buchempfehlung
Weiße, Christian Felix
Atreus und Thyest. Ein Trauerspiel in fünf Aufzügen
Die Brüder Atreus und Thyest töten ihren Halbbruder Chrysippos und lassen im Streit um den Thron von Mykene keine Intrige aus. Weißes Trauerspiel aus der griechischen Mythologie ist 1765 neben der Tragödie »Die Befreiung von Theben« das erste deutschsprachige Drama in fünfhebigen Jamben.
74 Seiten, 4.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten. Elf Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für diese preiswerte Leseausgabe elf der schönsten romantischen Erzählungen ausgewählt.
- Ludwig Tieck Die beiden merkwürdigsten Tage aus Siegmunds Leben
- Karoline von Günderrode Geschichte eines Braminen
- Novalis Heinrich von Ofterdingen
- Friedrich Schlegel Lucinde
- Jean Paul Die wunderbare Gesellschaft in der Neujahrsnacht
- Adelbert von Chamisso Peter Schlemihls wundersame Geschichte
- E. T. A. Hoffmann Der Sandmann
- Clemens Brentano Die drei Nüsse
- Ludwig Achim von Arnim Der tolle Invalide auf dem Fort Ratonneau
- Wilhelm Hauff Jud Süss
- Joseph von Eichendorff Das Schloß Dürande
442 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum



















