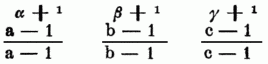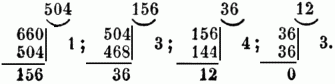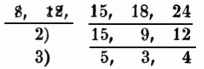Online-Bibliothek

Theiler

[465] Theiler, T. einer Zahl (Dividuus) heißt jede Zahl, welche in der zu theilenden aufgeht, wobei nur von ganzen Zahlen die Rede sein kann. Eine Zahl, welche außer 1 u. sich selbst keinen T. hat, heißt Primzahl, wie 2, 3, 5, 7, 11, 13 etc. Zwei od. mehre Zahlen, welche außer 1 keinen gemeinschaftlichen[465] T. haben, durch kein gemeinschaftliches Maß gemessen werden können, wie 15 u. 16,8 u. 9 etc. heißen relative Primzahlen. Eine zusammengesetzte Zahl ist dagegen eine solche, welche außer der 1 u. sich selbst wenigstens noch zwei T. hat, wie z.B. 14, die durch 7 od. 2 theilbar ist. Jeder T. einer zusammengesezten Zahl, welcher eine Primzahl ist, wird ein Primfactor derselben genannt. Man findet die Primfactoren einer gegebenen Zahl, wenn diese successiv durch alle Primzahlen dividirt wird, bis man auf einen Quotienten kommt, welcher selbst eine Primzahl ist. Sollen alle T. einer Zahl gefunden werden, so hat man nur die Combinationen aller Klassen von den Primfactoren der Zahl zu bilden, jedoch so, daß jeder so oft gesetzt werden darf, als sein Exponent Einheiten enthält, was man auch Combinationen mit eingeschränkten Wiederholungen nennt. So haben z.B. die Zahlen 60 u. 360 sehr viele T., weswegen dieselben schon im Alterthume bei der Eintheilung des Kreises zum Grunde gelegt worden. Es ist 60 = 2². 3. 5 u. 360 = 2³. 3². 5. Die sämmtlichen T. von 60 sind: 2, 3, 5; 2. 2, 2. 3, 2. 5, 3. 5; 2. 2. 3, 2. 2. 5, 2. 3. 5 u. außerdem 1 u. 2. 2. 3. 5, d.i. 60 selbst. Für 360 erhält man ebenso: 2, 3, 5; 2. 2, 2. 3, 2. 5, 3. 3, 3. 5; 2. 2. 2, 2. 2. 3, 2. 2. 5, 2. 3. 3, 2. 3. 5, 3. 3. 5; 2. 2. 2. 3, 2. 2. 2. 5, 2. 2. 3. 3, 2. 2. 3. 5, 2. 3. 3. 5; 2. 2. 2. 3. 3, 2. 2. 2. 3. 5, 2. 2. 3. 3. 5 u. 2. 2. 2. 3. 3. 5, so daß man der Reihe nach 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 u. 180 zu T. von 360 erhält. Die Summe aller T. einer Zahl zu finden, vermehre man den Exponenten jedes Primfactors um 1, vermindere die erhaltene Potenz um 1 u. dividire den Rest durch den um 1 verminderten zugehörigen Primfactor. Dann ist das Product dieser Quotienten der verlangten Summe gleich. Von N = a^α b^β c^γ ist die Summe aller T.

Von 360 ist z.B. die Summe aller oben genannten T., die 1 u. 360 mitgerechnet.

Es kann ferner zu 2 (od. mehrern) Zahlen ein gemeinschaftlicher u. insbesondere der größte gemeinschaftliche T. gesucht werden. Zu diesem Zwecke dividire man mit der kleineren von beiden in die größere. Geht die Division auf, so ist natürlich die kleinere Zahl der größte gemeinschaftliche T.; geht sie nicht auf, so dividire man mit dem Reste in den vorigen Divisor, u. wenn wieder ein Rest bleibt, mit diesem wieder in den vorhergehenden Divisor u. s. s., bis die Division (was wegen der ganzen Zahlen immer geschehen muß) einmal aufgeht. Der letzte Divisor ist der größte gemeinschaftliche T. Sind drei Zahlen gegeben, so sucht man ihn erst zur ersten u. zweiten, u. hierauf zu dem gefundenen T. u. zu der dritten Zahl ebenso; so ist das Verlangte geleistet. Beispiel: Es sei der größte T. zu 504 u. 560 gesucht:

Der letzte Divisor 12 ist die größte Zahl, welche in 504 u. 660 zugleich aufgeht. Dieses Verfahren wendet man an, um zu sehen, ob u. durch welchen größten T. sich ein Bruch heben läßt. Eine andere die T. betreffende Aufgabe ist, die kleinste Zahl zu suchen, welche beliebige gegebene Zahlen zu T-n hat. Man zerlege jeden T. in seine Primfactoren u. bilde aus den höchsten Potenzen jedes derselben ein Product, so ist dieses die verlangte durch alle gegebenen Zahlen theilbare Zahl. Zu 8 = 2², 12 = 2². 3, 15 = 3. 5, 18 = 2. 3², 24 = 2³. 3 ist der kleinste gemeinschaftliche Dividuus 2³. 3². 5 od. 360, weil 3, 2, 1 die höchsten vorkommenden Potenzen von 2, 3 u. 5 sind. Da 12 u. 8 in 24 aufgehen, so konnten diese auch vor der Zerlegung in die Primfactoren weggelassen werden. Hat man keine Factorentafeln, so wird die Rechnung oft so angesetzt, was nach dem Obigen keiner weitern Erklärung bedarf:

dann ist 2. 3. 5. 3. 4 die gesuchte Zahl. Um zu zwei Zahlen den kleinsten Dividuus zu suchen, dividire man mit dem größten gemeinschaftlichen T. beider in eine derselben u. multiplicire den Quotienten mit der andern. In der Bruchrechnung wird dieses Verfahren angewendet, um die Brüche auf die einfachste Weise in andere von einerlei Nenner zu verwandeln. Dann wird der kleinste gemeinschaftliche Dividuus aller Nenner der Generalnenner genannt. Eine andere Anwendung findet dieser wichtige Satz bei der Auflösung von Gleichungen mit mehren Unbekannten nach der Subtractionsmethode. Endlich ist es auch, bes. bei Untersuchungen über die Perioden der Decimalbrüche (s. Decimalbruch), wichtig zu bestimmen, wie viel Zahlen es gibt, welche kleiner sind als eine gegebene, u. welche mit dieser keinen gemeinschaftlichen T. haben. Sind a, b, c Primzahlen u. ist die gegebene Zahl N = a^α b^β c^γ, so ist die gesuchte Anzahl =

Z.B. gibt es 360. ¹/₂. ₂/³. ⁴/₅ d.i. 99 Zahlenwelche kleiner als 360 u. zu 360 relative Primzahlen sind. Das älteste Werk, welches Untersuchungen über die Primzahlen enthält, sind Euklids Elemente. Die meisten Entdeckungen in diesem Zweige machte Fermat.