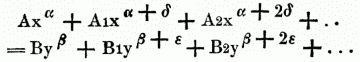Online-Bibliothek

Reihe

[2] Reihe, 1) mehre in einer Linie neben einander befindliche Dinge; 2) das Aufeinanderfolgen nach festgesetzter Ordnung; 3) jede Folge von Größen (die Glieder [Termini] derselben genannt), welche nach einem bestimmten Gesetz gebildet sind. Die R-n zerfallen in zwei Klassen, niedere od. einfache R-n (Progression), wo jedes Glied aus dem vorhergehenden durch Addition einer gewissen Größe (arithmetische Progression) od. durch Multiplication mit einer gewissen Größe (geometrische Progression) entsteht, od. doch die Bildungsweise aus diesen beiden Operationen nur zusammengesetzt ist; u. höhere od. analytische R-n, welche nach irgend einem complicirteren Gesetze gebildet sind; doch haben diese letzteren das gemeinschaftlich, daß alle Glieder einer R. eine gewisse Größe mit regelmäßig steigenden Exponenten enthalten, verbunden mit gewissen gesetzmäßig gebildeten Coefficienten, z.B.

auch daß alle Glieder neben solchen Coefficienten eine trigonometrische Function eines regelmäßig wachsenden Vielfachen eines u. desselben Bogens enthalten. Die Glieder einer R. werden von der Linken zur Rechten gezählt. Das am weitesten links stehende, von dem man ausgeht, heißt das Anfangsglied. Die Zahl, welche von einem Gliede angibt, das wievielte es vom Anfangsgliede an gezählt in der R. ist, heißt die Stellenzahl (Zeiger, Index) desselben. Wird bei einer R. irgend ein Glied als das letzte betrachtet, so heißt sie endlich, wie a³ + a²b + ab² + b³; dagegen unendlich, wenn dies nicht der Fall ist, wie in ¹/_1-x = 1 + x + x² + x³ +..... Der analytische Ausdruck eines unbestimmten Gliedes durch die unbestimmte Zahl seiner Stelle od. überhaupt durch das zugehörige Glied einer arithmetischen R., heißt das allgemeine Glied (Terminus generalis) der R. Der Coefficient dieses allgemeinen Gliedes wird ebenso der allgemeine Coefficient genannt. Ist eine unendliche R. so beschaffen, daß, je mehr Glieder derselben in ein einziges Ganzes vereinigt werden, der so erhaltene Ausdruck sich einem bestimmten Werthe ohne Ende immer mehr nähert, so nennt[2] man diesen Werth die Summe der R. u. diese R. selbst eine convergente (convergirende); findet dies nicht statt, so heißt sie divergent (divergirend) u. eine solche hat keine angebbare Summe. So ist z.B. 1 + x + x² + x³ +... in inf. für x = ¹/₂ convergent, nämlich = 2, für x = 1 od. x größer als 1, jedoch divergent, denn die Summe wächst für eine unbegrenzte Gliederzahl in das Unendliche. Ebenso ist sie für x = -1 divergent, denn die Summe schwankt zwischen 1 u. 0, je nachdem man eine ungerade od. gerade Anzahl von Gliedern summirt. Eine R. muß erst genau untersucht werden, ob sie convergirend od. divergirend ist, im letzteren Falle ist sie zu analytischen Untersuchungen nicht zu gebrauchen. Das summarische Glied (Terminus summatorius) einer R. der ersten Klasse ist der analytische Ausdruck für das Aggregat der Glieder derselben, vom Anfangsgliede an bis zu dem allgemeinen Gliede einschließlich. Die aus den successiven summatorischen Gliedern gebildete R. heißt die summirende R. (Series summatrix) od. Summenreihe der ersteren; ist z.B. gegeben: 1; 4; 7; 10; 13; 16, so ist 1; +5; +12; +22; +35; +51 eine R. 2. Ordn., 1; +6; +18; +40; 75; +126 der 3. Ordn. etc. Die arithmetische Progression erster Ordnung hat folgende allgemeine Form: a, a + d, a + 2d, a + 3d, ...... a + (n-1) d. Gelten die oberen Vorzeichen, so ist die R. steigend, die unteren: fallend; wird nun eine andere Größe, a, nach u. nach um die Summe der einzelnen Glieder der vorigen vermehrt, so entsteht eine arithmetische R. zweiter Ordnung etc. In jeder arithmetischen Progression sind fünf Größen vorhanden, die in solcher Beziehung zu einander stehen, daß wenn drei von ihnen gegeben sind, die beiden anderen daraus hergeleitet werden können, sie sind: a das Anfangsglied, d die Differenz der R., z das Endglied, n die Anzahl der Glieder u. s die Summe aller Glieder. Die beiden Hauptformeln, aus denen die übrigen leicht abgeleitet werden können, sind hierfür z = a ± (-1) d u. s = ⁿ/₂(a+z). Die geometrische Progression hat folgende allgemeine Form: a, ae, ae², ae³, ... ae^n-1 ist e größer als 1, so ist sie steigend, ist e kleiner als 1, so ist sie fallend. Auch hier hat man fünf Größen, die außer e, was hier der Factor od. der Exponent der R. heißt, wie oben bezeichnet werden u. die durch folgende Formeln unter einander zusammenhängen: z = ae^n-1 u. s = a (eⁿ-1)/(e-1), woraus die übrigen sich wieder leicht ableiten lassen. Bildet man die successiven Producte aus den 1, 2, 3,_... n ersten Gliedern einer gemeinen arithmetischen R.: z.B. a; a (a+b); a (a+b)(a+2b); ... a(a+b)(a+2b) ... (a+[n-1]b), so nennt man die so entstehende R. eine hypergeometrische od. geometrische zweiter Ordnung. Die einzelnen Glieder derselben führen den Namen numerische Facultäten der factoriellen od. Factorenfolgen. Für b = o geht die R. in eine gemeine geometrische über. Die rücklaufenden (recurrirenden, recurrenten) R-n sind eine Folge von Größen, wo jede aus den n vorhergehenden dadurch hervorgebracht wird, daß man rückwärts die letzte, vorletzte, vorvorletzte etc. beziehungsweise mit der ersten, zweiten, dritten, ..., nten von n unveränderlichen gegebenen Zahlen multiplicirt u. das Aggregat dieser Producte nimmt. Die zuletzt genannten n unveränderlichen Größen in ihrer Gesammtheit werden die Beziehungsscale (Scala relationis) od. das Beziehungsmaß der R. genannt. Die reciproken R-n sind R-n solcher Quotienten, welche bei einem unveränderlichen Dividendus zu Divisoren die auf einander folgenden Glieder einer arithmetischen R. von irgend einer Ordnung haben. Sind die Divisoren die Glieder einer gemeinen arithmetischen R., so stehen je drei auf einander folgende Glieder in stetiger harmonischer Proportion, u. die R. heißt dann eine harmonische Progression; eine solche ist 1, ¹/₂, ¹/₃, ¹/₄, ¹/₅, ¹/₆ etc. Die R-n der zweiten Klasse dienen, einen genäherten Werth einer Größe anzugeben, welchen man sonst entweder gar nicht, od. nur unter einer sehr verwickelten Gestalt erhalten kann. Außerdem lassen sich über R-n als Formen einer Größe, überhaupt merkwürdige Untersuchungen anstellen, in Absicht auf die Entwickelung ihrer Glieder, die allgemeine Form derselben, die Summe der Glieder u. die Vergleichungen verschiedener R-n unter einander. Hierher gehören: der Binomische u. Polynomische Lehrsatz, die Cyklometrischen u. Logarithmischen R-n, die Bernouillische, die Maclaurinische, ferner die R., welche der Taylorsche Lehrsatz enthält, die Kettenbrüche. Ferner gehört hieher, was man die Umkehrung der R-n (Reversio s. Inversio serierum, Retour des suites) nennt. Man verstand darunter Anfangs die Auflösung folgender Aufgabe. Wenn y durch eine nach Potenzen von x fortschreitende R. gegeben ist, umgekehrt x durch eine nach Potenzen von y fortschreitende R. auszudrücken. Dieselbe wurde aber später dahin erweitert: Aus der allgemeinen Gleichung zwischen x u. y

einen nach Potenzen von y fortschreitenden Ausdruck für irgend eine Potenz von x, z.B. für x^μ abzuleiten. Der einfachste eben erwähnte Fall des Reversionsproblems ist schon von Newton untersucht worden; in größerer Allgemeinheit aber hat sich zuerst Moivre mit demselben beschäftigt; eine einfache Formel hat Tempelhoff in seiner Analysis endlicher Größen gegeben; eine Entwickelung der Umkehrungsreihe machte zuerst H. C. W. Eschenbach (De serierum reversione etc., Lpz. 1789), bekannt, wozu A. Rothe (Formulae de serierum reversione etc., Lpz. 1793) den Beweis gab. Wie dieser, so wies auch Hindenburg seinerseits den Zusammenhang des Reversionsproblems mit dem Polynomischen Lehrsatze nach (Problema solutum ad serierum reversionem etc., Lpz. 1793). Die Ableitung der Rotheschen Formel aus dem la Grangeschen Lehrsatze hat E. G. Fischer (in seiner Theorie der Dimensionszeichen) u. I. F. Pfaff (in seiner Disquisitiones analyticae, Helmst. 1797) gegeben, F. Sarus aber (in Application du calcul aux différences partielles à la résolution de quelques problèmes d'analyse) eine Entwickelungsweise des Reversionsproblems mitgetheilt, welche das Gesetz der Entwickelung sehr einfach darstellt. Vgl. Summirung der Reihen. 4) (Her.), bei den in fünf R-n getheilten Schilden nannte man die oberste die Haupt-, die zweite die Ehren-, die dritte die Band-, die vierte die Nabel- u. die fünfte die Fußreihe; jetzt bezeichnet man sie häufiger mit [3] Zahlen. Wird ein Mittelschild auf die Nabelreihe gesetzt, so nennt man ihn auch Nabelschild u. die Stelle, welche er einnimmt, Nabelstelle; 5) Metrische, Rhythmische R-n, s.u. Poetik C).