Arbeit [1]
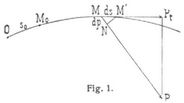
[266] Arbeit. Das Produkt Pdp aus der Größe P einer Kraft und der Projektion dp des von ihrem Angriffspunkt M zurückgelegten Wegelementes ds auf die Richtung der Kraft heißt die Elementararbeit der Kraft P längs des Wegelementes ds (Fig. 1).
Ist Pt die Projektion von P auf die Richtung des Bogenelementes (Tangente der Bahn), so wird Pdp = Ptds, d.h. die Elementararbeit der Kraft P ist gleich dem Produkt aus ihrer Tangentialkomponente Pt und dem Wegelemente ds selbst (weil nämlich die Endpunkte von P und Pt, sowie die von ds und dp auf einem Kreise liegen). Ist α der Winkel, den die Kraft P mit der Tangente der Bahn bildet, so ist
P cos α ds = Pdp = Ptds.
Das Produkt aus zwei Strecken und dem Cosinus ihrer Neigung gegeneinander nennt man das geometrische (skalare) Produkt der beiden Strecken, oder nach Graßmann das innere Produkt derselben.
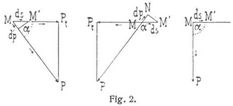
Ist (Fig. 2) der Winkel α spitz, so haben Pt und ds und ebenso P und dp gleichen Sinn und die Elementararbeit ist positiv. Ist α stumpf, so haben ds und Pt, sowie P und dp entgegengesetzten Sinn; die Elementarbeit ist negativ; ist endlich a = 1/2π, so leistet die Kraft keine Arbeit. Ist der Winkel α gleich Null oder π, so ist die Elementararbeit Pds oder –Pds, d.h. gleich dem positiven oder negativen Produkt der Kraft und des Elementarweges, da P mit seiner Projektion Pt zusammenfällt.
Die Kraft P kann die Resultante von andern Kräften P(1), P(2) ..., P(i) ..., P(n) sein; sie ist dann die Schlußlinie eines Kräftepolygons, und ihre Projektion auf die Tangente ist die Summe der Projektionen ihrer Komponenten, d.h. es ist
und wenn man diese Gleichung mit dem Wegelemente ds multipliziert, so folgt, daß die Elementararbeit der Resultanten von Kräften, die an einem Punkt angreifen, gleich der Summe Elementararbeiten der Komponenten ist.
Ist ferner das Wegelement ds die Resultante der Wegelemente ds1, ... ds2, ... dsi, ... dsn eine Reihe von Bewegungen, aus denen die Bewegung des Angriffspunktes der Kraft P zusammengesetzt ist, so ist ds die Schlußlinie eines Polygons des ds1 und folglich
dp = dp1 + dp2 + ... + dpi + ... + dpn.
Die Multiplikation dieser Gleichung mit P zeigt, daß die Elementararbeit einer Kraft längs eines Wegelementes, das aus einer Reihe von Bewegungen entspringt, gleich der Summe der Elementararbeiten der Kräfte längs den Wegelementen der einzelnen Bewegungen ist.
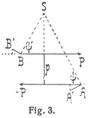
Die Summe der Elementararbeiten der beiden Kräfte eines Paares ist für jede Translationsverschiebung Null. Um sie für. eine Windungsbewegung zu finden, zerlege man die durch sie erfolgende Verschiebung der Angriffspunkte in die Translationsverschiebung und die Rotationsverschiebung; erstere liefert Null; in bezug auf letztere spalte man die Rotation in eine solche um eine zur Ebene des Paares senkrechte und eine in dessen Ebene hineinfallende Achse. Ist S (Fig. 3) der Schnittpunkt der Achse mit der Ebene des Paares, so gibt die erstere, wenn dϑ die Amplitude ist, die beiden Verschiebungen der Angriffspunkte A und B, nämlich AA' = SA∙dϑ, [266] BB' = SB∙dϑ und wenn ψ, ψ' die Winkel sind, die SA und SB der Richtung der Kräfte bilden, so werden die Projektionen mit derselben SA∙dϑ sin ψ und SB∙dϑ∙sinψ'; daher die Arbeiten P∙SA∙dϑ sin ψ und P∙ (– SB∙dϑ∙sinψ'); daher ihre Summe
Pdϑ (SA · sin ψ – SB · sinψ') = Ppdϑ.
Die Elementararbeitssumme für die Rotation um die in die Ebene des Paares fallende Achse ist Null, weil die Verschiebungen der Punkte A und B senkrecht zur Richtung der Kräfte sind. Daher bleibt für Summe der Elementararbeiten der Kräfte eines Paares (P, –P) der Ausdruck Ppdϑ, wo dϑ die Amplitude der Rotationskomponenten ist, deren Achse senkrecht zur Ebene des Paares. Ist α der Winkel der Achsen des Paares und der Windung, dσ die Amplitude der letzteren, so wird dϑ = dσ cos α, mithin die Elementararbeit Ppdσ cos α, d.h. gleich dem geometrischen (skalaren) Produkt des Achsenmoments des Paares und der auf der Windungsachse aufgetragenen Amplitude dσ der Windung.
Die Summe aller Elementararbeiten einer Kraft P längs eines Weges M0M (Fig. 1 u. 2) ihres Angriffspunktes heißt die Totalarbeit der Kraft P längs dieses Weges. Rechnet man die Wege s von irgend einem Anfangspunkte O der Bahn des Angriffspunktes, so wird die Totalarbeit T durch das Integral (Arbeitsintegral, Linienintegral der Kraft längs des Weges)
dargestellt. Hierin sind P und cos η als Funktionen von s auszudrücken. An Stelle des Bogens s kann auch eine andre Integrationsvariable treten, wobei sich die Grenzen des Integrals entsprechend ändern.
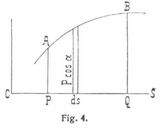
Stellt man P cos α als Ordinate einer Kurve dar (Fig. 4), entsprechend der Variabeln s als Abszisse, so drückt die Fläche PABQ der Kurve, begrenzt von dieser, dem Stück PQ = s – s0 der Abszissenachse und den Ordinaten, entsprechend den Integrationsgrenzen s = s0 und s = s die Arbeit dar. Ist P nach Größe und Richtung konstant, so wird
d.h. gleich dem Produkte aus der konstanten Intensität der Kraft und der Projektion des Bogens s–s0 auf die Richtung der Kraft. Dies ist z.B. bei der Schwere der Fall. Man unterscheidet zwischen virtueller und aktueller (reeller) Elementararbeit, je nachdem das Wegelement, um das der Angriffspunkt der Kraft verschoben wird, von demselben nicht wirklich durchlaufen, sondern nur als möglicherweise beschreibbar oder als wirklich beschriebenes Bahnelement aufgefaßt wird.
Weiteres über Bestimmungsmethoden der Arbeit und Arbeitssumme s. Kräftefunktion. Die Beziehungen der Elementararbeitssumme eines Kräftesystems zum Gleichgewicht desselben s. Prinzip der virtuellen Geschwindigkeiten; die Beziehungen zur Bewegung der Systeme s. Prinzip der lebendigen Kraft.
(Schell) Finsterwalder.
Adelung-1793: Mosaische Arbeit · Musiv-Arbeit, die · Arbeit, die · Castōr-Arbeit, die
Brockhaus-1809: Musiv-Arbeit · Die Mosaische Arbeit
Brockhaus-1911: Kalte-Nadel-Arbeit · Getriebene Arbeit · Musivische Arbeit · Ritter der Arbeit · Recht auf Arbeit · Eingelegte Arbeit · Arbeit · Elektrische Arbeit · Florentiner Arbeit · Erhabene Arbeit
DamenConvLex-1834: Musivische Arbeit · Arbeit
Eisler-1904: Arbeit · Psychische Arbeit · Arbeit
Herder-1854: Getriebene Arbeit · Musivische Arbeit · Florentiner Arbeit · Arbeit · Eingelegte Arbeit
Kirchner-Michaelis-1907: Arbeit
Lueger-1904: Getriebene Arbeit · Eingelegte Arbeit · Innere Arbeit · Indizierte Arbeit, indizierter Effekt, indizierte Leistung · Disponible Arbeit · Aeußere Arbeit · Aequivalenz von Wärme und Arbeit · Cosmatus-Arbeit · Arbeit [2]
Meyers-1905: Eingelegte Arbeit · Effektive Arbeit · Elektrische Arbeit · Florentiner Arbeit · Erhabene Arbeit · Durchbrochene Arbeit · Abgesperrte Arbeit · à jour-Arbeit · Arbeit [1] · Dentelierte Arbeit · Arbeit [2]
Buchempfehlung
Diderot, Denis
Die Nonne. Sittenroman aus dem 18. Jahrhundert
Im Jahre 1758 kämpft die Nonne Marguerite Delamarre in einem aufsehenerregenden Prozeß um die Aufhebung ihres Gelübdes. Diderot und sein Freund Friedrich Melchior Grimm sind von dem Vorgang fasziniert und fingieren einen Brief der vermeintlich geflohenen Nonne an ihren gemeinsamen Freund, den Marquis de Croismare, in dem sie ihn um Hilfe bittet. Aus dem makaberen Scherz entsteht 1760 Diderots Roman "La religieuse", den er zu Lebzeiten allerdings nicht veröffentlicht. Erst nach einer 1792 anonym erschienenen Übersetzung ins Deutsche erscheint 1796 der Text im französischen Original, zwölf Jahre nach Diderots Tod. Die zeitgenössische Rezeption war erwartungsgemäß turbulent. Noch in Meyers Konversations-Lexikon von 1906 wird der "Naturalismus" des Romans als "empörend" empfunden. Die Aufführung der weitgehend werkgetreuen Verfilmung von 1966 wurde zunächst verboten.
106 Seiten, 6.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Biedermeier III. Neun weitere Erzählungen
Biedermeier - das klingt in heutigen Ohren nach langweiligem Spießertum, nach geschmacklosen rosa Teetässchen in Wohnzimmern, die aussehen wie Puppenstuben und in denen es irgendwie nach »Omma« riecht. Zu Recht. Aber nicht nur. Biedermeier ist auch die Zeit einer zarten Literatur der Flucht ins Idyll, des Rückzuges ins private Glück und der Tugenden. Die Menschen im Europa nach Napoleon hatten die Nase voll von großen neuen Ideen, das aufstrebende Bürgertum forderte und entwickelte eine eigene Kunst und Kultur für sich, die unabhängig von feudaler Großmannssucht bestehen sollte. Für den dritten Band hat Michael Holzinger neun weitere Meistererzählungen aus dem Biedermeier zusammengefasst.
- Eduard Mörike Lucie Gelmeroth
- Annette von Droste-Hülshoff Westfälische Schilderungen
- Annette von Droste-Hülshoff Bei uns zulande auf dem Lande
- Berthold Auerbach Brosi und Moni
- Jeremias Gotthelf Die schwarze Spinne
- Friedrich Hebbel Anna
- Friedrich Hebbel Die Kuh
- Jeremias Gotthelf Barthli der Korber
- Berthold Auerbach Barfüßele
444 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum